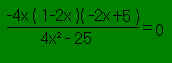
Réalisé de A à Z par des élèves en classe de seconde |
CHAPITRE 5: Equations et InéquationsParagraphe 5)Résolution d'équations avec des quotients.LENIN ClémentGELE Jean-BaptisteMALOSZYC Milan Classe de seconde 5 |
Amiens
Somme Picardie |
Méthode de résolution d'équations (avec quotients) qui ne sont pas du premier degré.
1) Rechercher les valeurs interdites. On cherche l'ensemble de définition.
2) On fait passer tout à gauche pour avoir "= 0" ( égale à zéro ) à droite.
3) On doit avoir un seul quotient, pour cela on utilise la mise au même dénominateur.
4) Factoriser ( le membre de gauche )
5) On utilise la propriété du ou des quotients nuls.
6) On vérifie si les solutions ne sont pas interdites ( voir avec le 1) )
7) On écrit les solutions ( S={...} )
Exemple:
résoudre
:
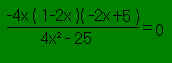
recherche des valeurs interdites :
-4x(1-2x)(-2x+5)
-4x²-25
Les valeurs interdites sont:
4x²-25=0 interdit
(2x)²-(5)²=0
(2x-5)(2x+5)=0
x=5/2 ou x= -5/2 sont des valeurs interdites
Ensemble de définition D = R / { 5/2 ; -5/2 }
Donc x appartient à ] - 00 ; -5/2 [ U ] -5/2 ; 5/2 [ U ] 5/2 ; +00 [
x appartient à D quand :
x n'égale pas 5/2 et x n'égale pas -5/2
L'équation est équivalente à
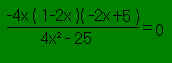
avec x n'est pas égal à 5/2 et x n'est pas égal à -5/2
Propriété du quotient nul:
Un quotient est nul si et seulement si son numérateur est nul.
-4x ( 1-2x )( -2x+5 ) = 0
-4x = 0 donc x = 0
ou
1-2x = 0 donc x = 1/2
ou
-2x+5 = 0 donc x = 5/2
On vérifie que les solutions ne sont pas interdites
5/2 n'appartient pas à D
S ={ 0 ; 1/2 ; 5/2 }
5/2 est une valeur interdite donc
S = { 0 ; 1/2 }
-----------------------------------------
Exercice :
Résoudre:
![]()
Correction:
![]()
les valeurs interdites sont x = 1 car (x-1) = 0 interdit
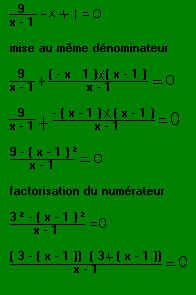
donc
(4-x)(2+x) est
nul
x-1
4-x=0 ou 2-x=0
x=4 ou x=2
et ces valeurs ne sont pas interdites
S={ 2 ; 4 }