SENS DE VARIATION

Il existe deux sens de variations différents :

1) f croissant sur I

on a : - Pour tout réel x1 et x2 de I

- Si (x1 + petit que x2 ) alors (f(x1) + petit ou égal a f(x2))

Exemples :

x et y varient dans le même sens

2) f décroissant sur I

on a : - Pour tout réel x1 et x2 de I

- Si (x1 + grand que x2 ) alors (f(x1) + grand que f(x2))

Exemples :

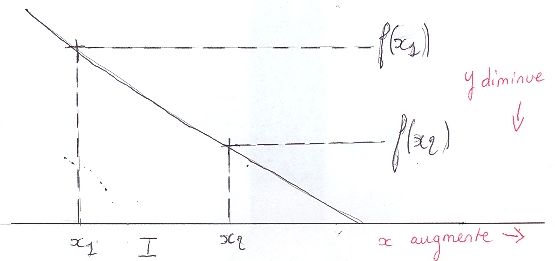
x et y ne warient pas dans le même sens

Nous allons étudiez le sens de variations d'une fonction f pour pouvoir ensuite etablir son tableau de variation


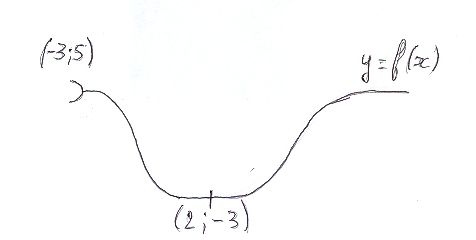
1 - Etudiez sens de variation de f

- f est décroissant sur ]-3 ; 2]

- f est croissant sur [2 ; + infinie [

nous pouvons a présent établir le tableau de variation de cette fonction f

MINIMUM - MAXIMUM

Voici une fonction f sur ]-1 ; 6 ]



Le maximum de la courbe f est 5 atteint pour x en 6

Le minimum de la courbe f est -3 atteint pour x en 2

Voici les définitions de minimum et de maximum

1} Maximum

La fonction f admet un maximum en a sur I lorsque pour tout x de I , f(x) + petit
ou égal à f(a) . le réel f(a) est le maximum de f sur I .

2} Minimum

La fonction f admet un minimum en a sur I lorsque pour tout x de I , f(x) +grand
ou égal a f(a) . Le réel f(a) est le minimum de f sur I .