Intervalle	Ensemble des réels x tels que...	Représentation graphique
[a;b] fermé	axb
[a;b[	ax<b
]a;b[ ouvert	a<x<b
[a;+[	xa
]-;b]	x<b

Définition:

Soit I et J deux intervalles:

• L'ensemble des réels qui appartiennent à la fois à I et à J est appelé l'intersection de I et de J. Cet ensemble est noté I J.

• L'ensemble des réels qui appartiennent à I ou à J ou aux deux à la fois est appelé la réunion de I et de J. Cet ensemble est noté I U J.

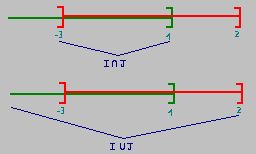
Exemple : pour I=[-2;3[ et J=]-4;1]

on a I J=[-2;1]

et I U J=]-4;3[

Comment utiliser les intervalles?

Exercice

a- Dans chacun des cas, dire à quel intervalle appartient le réel x, puis le dessiner: -1x<2 ; 1/2x3 ; x>4

b- Traduire par des inégalités l'appartenance du réel x à chacun des intervalles suivants: I=]-3;2] ; J=]-;1]. Déterminer l'ensemble
I J et l'ensemble I U J.

Solution

a- -1x<2 se traduit par x appartient à [-1;2[

1/2x3 se traduit par x appartient à [1/2;3]

x>4 se traduit par x appartient à ]4;+[

b- x appartient à ]-3;2] se traduit par-3<x2

x appartient à]-;1] se traduit par x1

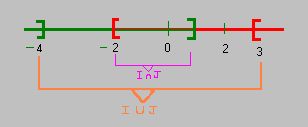
Méthode: Pour trouver la réunion ou l'intersection de deux intervalles, la représentation des intervalles sur un axe est très utile.

Les réels appartenants à I J sont ceux qui appartiennent à la fois à I et à J; ce sont donc les réels qui correspondent à la partie colorée des deux couleurs; on a donc I J=]-3;1].

Les réels appartenant à I U Jsont ceux qui appartiennent à I ou à J; c'est-à-dire ceux qui correspondent à la partie colorée par au moins l'une des couleurs; on a donc I U J=]-;2].